Machine Learning

Computers can learn like human beings, from observations, examples, images, sensors, data, and experience. Machine learning is a field of artificial intelligence that involves the design and implementation of algorithms for computers to evolve their behavior from observations, examples, images, sensors, data, and experience, among many other sources. My main research in machine learning is on pattern recognition, dimensionality reduction, representation learning, and clustering.

The main focus of my research in this area is to devise efficient algorithms for classification, clustering, feature selection, dimensionality reduction, visualization and performance evaluation, with applications to interactomics, transcriptomics and multi-omics data integration. Over the past 15 years, I have contributed quite a bit in many application areas (mainly in transcriptomics and interactomics) as can be seen below. In fundamental pattern recognition I have worked in statistical pattern recognition. A summary of my contributions is given below. Some items are just summarized in a sentence or two; more information can be found in the corresponding publications.

Optimal 1D Clustering + KPCA

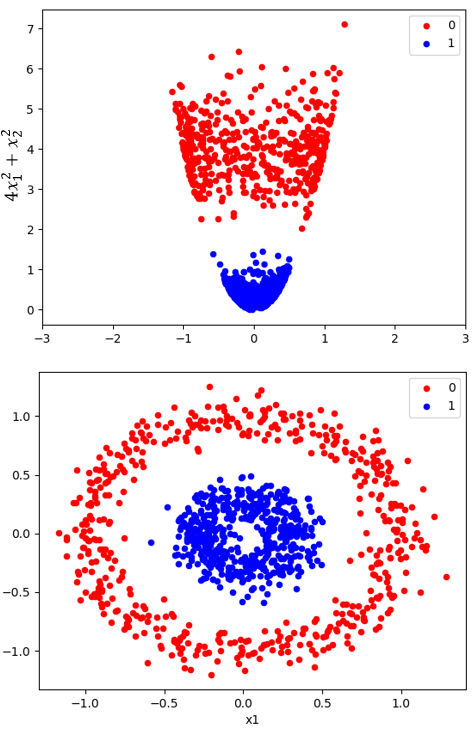
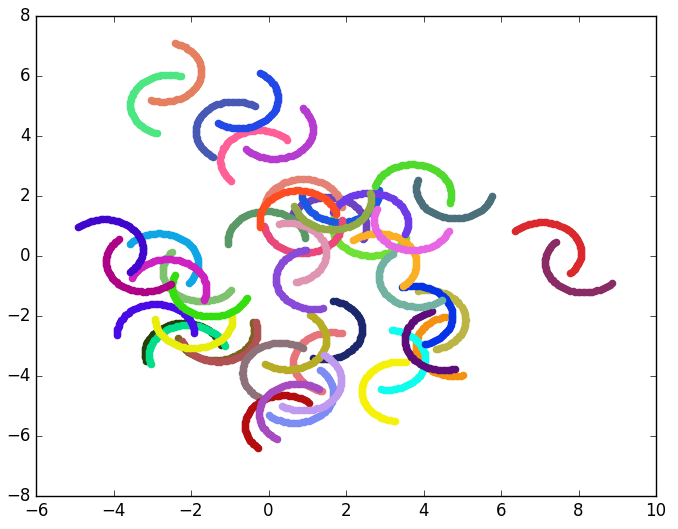We have recently proposed a nonlinear dimensionality reduction and clustering approach based on kernel PCA and one-dimensional, optimal multi-level thresholding. The algorithm consists of utilizing kernel PCA to reduce the data onto the one-dimensional space. An optimal multi-level thresholding algorithm is then applied to the 1D data along with indices of validity to discover the optimal clustering. As the algorithm runs in quadratic time, it allows to explore a wide range of parameters of the kernels, making it more efficient than using k-means combined with other non-linear dimensionality methods or even KPCA. Results on synthetic data (figure on the right) and images of the 26 letter alphabet from MNIST show Silhouette scores higher than 0.98, which makes it a very competitive approach for clustering high-dimensional, complex data.

Relevant publications:

• To be updated.

Summary of Previous Contributions

• We have proposed a polynomial-time algorithm for finding an optimal multilevel thresholding of irregularly sampled histograms. The proposed framework has quite important applications in texture recognition, biofilm image segmentation, and, in particular, it is able to optimally cluster data in one dimension, and in polynomial time. We have extended this algorithm to a sub-optimal multi-level thresholding algorithm for finding binding sites in ChIP-seq data (see Transcriptomics).
• We have proposed a new linear dimensionality reduction method that maximizes the Chernoff distance in the transformed space. The method has been shown to outperform the traditional linear dimensionality reduction schemes such as Fisher's method and the directed distance matrices.
• We have found the necessary and sufficient conditions for which Fisher's discriminant analysis method is equivalent to Loog-Duin's linear dimensionality reduction.
• We have proposed a new family of weak estimators which perform very well in estimating non-stationary data. The estimators have been applied to adaptive data compression, news classification, and applications to detection of child pornography at the network level.
• We have devised a visualization scheme for analyzing fuzzy-clustered data. The scheme allows to show membership for k-fuzzy clustered data by projecting it onto a (k-1)-dimensional hypertetrahedron. Applications to fuzzy-clustered microarray data have been shown.
• I have proposed a model to selecting the threshold in Fisher's classifier. I have also studied the relationship between Fisher's classifier and the optimal quadratic classifier.
• I have found the necessary and sufficient conditions for selecting the best hyperplane classifier within the framework of the optimal pairwise linear classifier.
• We have developed the formal theory of optimal pairwise linear classifiers for two classes represented by two dimensional normally distributed random vectors. The formal theory has also been extended for d-dimensional normally distributed random vectors, where d>2.
• We are currently developing approaches for linear dimensionality reduction (LDR) used for classification and feature selection.
• We have proposed a new approach that combines non-linear mapping on LDR with applications to class-imbalance problems present in prediction of microRNA and high throughput protein-protein interactions.